Simple Excel calculation of market basket analysis, I mean cross sell / up sell, I mean if someone buys A, will he buy B?
You can download here a table calculating combinations of items appearing frequently on the same orders.
It can be very useful to know, that customer, buying product A, is likely to buy product B – so you can successfully propose it to him.
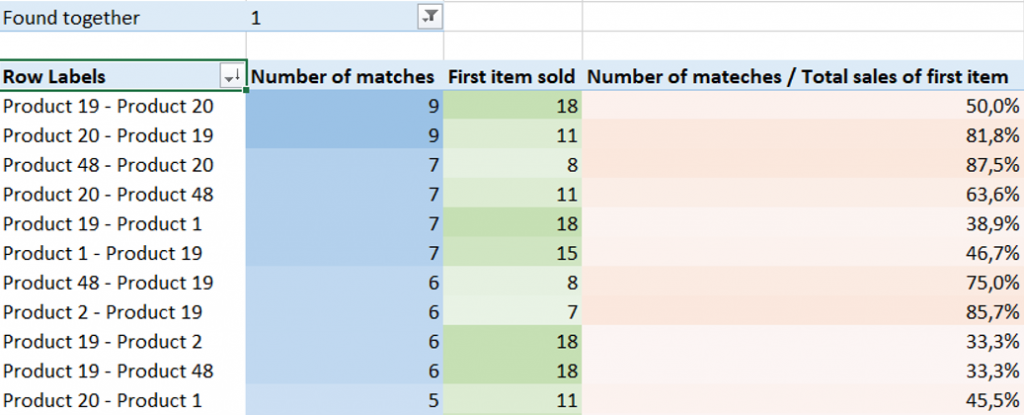
Model uses Power Query and Power Pivot.
You can use it without deep understanding – just replace the sample data with yours and refresh.
This model is quite demanding on computer performance. If you had some idea how to make it more effective, please let me know.
Files to download:

Hi,
Thanks for sharing the .xls file.
Is there a way to also find the combinations of 3, 4, 5, … articles in the same basket?
regards,
In this case I´d recommend already prepared R-packages and run it in R.
hi,
i want to know how can i make the raw data to combination
and i see some Number of mateches / Total sales of first item over %
seems not logical :
https://imgur.com/AkAHx8J
appreciate you sharing
i figured it out,
i think the 【all】 data ,should remove duplicate first,or the formula = Number of mateches / Total sales of first item over will over 100%.
second, because i use this on shopping basket , the two columns are consumer and product.
I want to know the feature of consumer , so i use this way.
🙂 thanks excel town
Hello there!
I have a question about this tamplate. Is it possible to add more then two matches?
For example, if I want to see ten matches of id in one order? Is it possible to edit this table this way?
Hi!
First of all, thank you so much for this.
Question:
It appears to me that the model is not working as intended if an order only contains ONE products – and no complementaries. It is my experience that orders with single products/items, are split across other orders with single products/items. I think so, because the model is telling me that products which have never been on the same order, is in fact sold together.
Do you know if I am right here :)?
Again, thanks!