Našimi kurzy prošlo více než 10 000+ účastníků
2 392 ověřených referencí účastníků našich kurzů. Přesvědčte se sami
Reference ze školení Středně pokročilý Excel (11/2023)
- Hezky a jednoduše podané příklady
- Přístup paní lektorky byl skvělý
- Zodpovězené dodatečné dotazy
- Skvělý a empatický přístup paní lektorky, naprostá spokojenost
Kurz:
Reference ze školení SQL (10/2023)
- Možnost sama si vše naklikat na PC
- Nezatěžování teorií
- Skvělé vedení kurzu i obsah
- Praktické zkoušení dotazů je super, odbočka k Power Query také
Kurz:
Reference ze školení PYTHON (09/2023)
- Byla jsem s pokojena s lektorem i organizací
- Seznámení a postupné ponoření do problematiky bylo skvělé
- Bavila mě především celá hlavní část kurzu
- Konkrétní příklady byly moc užitečné
- Ideální tempo, srozumitelnosti, praktické příklady
Kurz:
Reference ze školení Středně pokročilý Excel (09/2023)
- Super jsou příklady a cvičení
- Cokoliv nešlo, lektorka pomohla a poradila
- Výklad mentorky byl výborný
- Mnoho praktických příkladů
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (09/2023)
- Způsob vykládání, hodně příkladů, vše jsem si mohla vyzkoušet - vše velmi srozumitelné
- Vyhovovalo mi, že se vše dělalo na příkladech
- Jednoduché vysvětlení, možnost prakticky vyzkoušet
Kurz:
Reference ze školení Středně pokročilý Excel (08/2023)
- Rychlost výkladu akorát
- Dostatek příkladů a procvičování i opakování
- Super tempo
- Flexibilní pojetí výuky
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Středně pokročilý Excel (05/2023)
- Výborná lektorka
- Tempo přizpůsobené všem
- Člověk se nebál zeptat
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (05/2023)
- Kurz je dobře strukturovaný, moc mi to vyhovovalo
- Přístup lektora byl nápomocný, vše dobře vysvětlil
- Vhodné tempo, proaktivní přístup
Kurz:
Reference ze školení Středně pokročilý Excel (03/2023)
- Lektorka byla velmi ochotná
- Vše vysvětlovala v klidu, a když bylo potřeba, cokoliv zopakovala
- Velmi srozumitelné a dobře vysvětleno
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (02/2023)
- Vše bylo vyzkoušeno od úvodu
- Příjemné tempo práce
- Příjemný lektor ochotný vše vysvětlit
- Tempo tak akorát, perfektní přístup, vynikající znalosti
Kurz:
Reference ze školení Excelu pro labužníky (11/2022)
- Oceňuji - nachystané podklady, příklady využitelné v praxi
- Skvělé vychytávky, vyhovující tempo
- Skvělý lektor - profesionální, sympatický
Kurz:
Reference ze školení Úvod do Power BI (11/2022)
- Vše zkoušíme, méně teorie
- Každý zádrhel se vysvětlí :-)
- Praktické příklady, možnost si vše vyzkoušet, tempo lektora - vše super!
- Rychlost je odpovídající náročnosti a zkušenosti školených
- Interaktivita, ukázky chyb (na co si dát pozor), výklad byl jasný a přehledný
- Výborné tempo, skvělý přístup, vynikající znalosti
Kurz:
Reference ze školení Power Query a Power Pivot (10/2022)
- Srozumitelnost přednosu
- Hodně praxe tj.super
- Výborné zkušební příklady
- Tipy v Power Pivot
Kurz:
Kurz Power Query a Power Pivot
Reference ze školení Středně pokročilý Excel (10/2022)
- Pro mě velmi obohacující.
- Spoustu typů a vychytávek. Příjemná lektorka.
- Dostatek času procvičit příklady
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Excelu pro BENU Lékárna (09/2022)
- Lektor byl velmi komunikativní a nápomocný. Kdykoli někdo potřeboval, aby lektor zpomalil, tak ochotně cely usek zopakoval.
- Získal jsem základní přehled o Excelu, Zatím jsem byl samouk.
- Vše super
Reference ze školení SQL (02/2022)
- Výborný a zrozumiteľný spôsob podania
- Paní Šperková velice pěkně vysvětluje a vše je pochopitelné i pro začínající.
- Líbilo se mi podání kurzu ve smyslu příkladů, ukázek různých přístupů a návodů, jak v souvislosti s jazykem SQL přemýšlet. Dobré byly ukázky příkazů pro práci s čísly a textovými řetězci. Výklad byl velmi srozumitelný.
Kurz:
Reference ze školení Excelu (01/2022)
- Oceňuji, že lektor souběžně komentuje, co dělá a promítá to na sdílenou obrazovku, rovněž oceňuji tempo celého procesu
- Jsem začátečník, moc se mi to líbilo.
- Praktické příklady jsou vždy lepší než teorie, takže super.
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (11/2021)
- Za mě dobře vyvážený obsah a vše dobře vysvětleno, dost prostoru na dotazy, dobře připravené příklady.
- Oceňuji, že lektor po krátkém teoretickém úvodu hned přešel k praktickým cvičením, na kterých si člověk mohl lépe uvědomit možnosti programu a principy na kterých pracuje.
- Nemám, co vytknout, je to super :)
Kurz:
Reference ze školení Excelu (11/2021)
- Moje první celodenní školení on line, byla jsem spokojená
- Kurz byl skvělý (není co vytknout, tak alespoň maličkosti :) ), moc děkuji.
- Pan lektor problematiku zná, pracuje s ní v praxi, umí bezvadně podat, nemám jedinou výhradu. Obávám se že není moc prostoru pro další zlepšení.
- Školení mi přineslo to, co jsem očekávala - rozšíření znalostí z excelu, poznání nových funkcí a návod, jak ty stávající používat lépe. Ukázka z Power Pivot mě nalákala na další školení :-)
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Excelu (10/2021)
- Jednotlivé funkce Excelu byly prezentovány názorně a zároveň srozumitelně. Lektorka volila tempo dle potřeb účastníků kurzu, byla velmi příjemná, ochotná pomoci a dovysvětlit.
- Skvěle zvolená struktura kurzu. Výklad jasný a pochopitelný. Velmi milá lektorka.
- Líbilo se mi že jsem si mohla vyzkoušet vše na PC. Pokud jsem měla problém, řešil se hned.
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Excelu (12/2020)
-
Není co vytknout - naprosto srozumitelný výklad.
-
Líbil se mi přístup k jednotlivcům a rady k našim individuálním požadavkům.
-
Líbil jsem mi výklad po obsahové stránce i způsob, jakým byl podán.
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (9/2020)
- Kurz se mi celkově velmi líbil. Přišla mi dobrá struktura, posloupnost i množství informací
- Dobrý výklad látky, skvělé praktické příklady a ukázky, tipy a triky
- Jasná struktura kurzu - Vizuály / Datový model / Power Query
- Bylo to praktické. Pomůže mi to optimalizovat už vytvořené dotazy
Kurz:
Reference ze školení Excel pro začátečníky (6/2020)
- Vše v nejlepším pořádku.
- Výborný výklad, příklady, odpovědi na otázky...
- Skvělá školitelka, vše bylo srozumitelné.
- Super výuka, nic bych neměnila.
- Základy vysvětleny jednoduše a pochopitelně, dostatek času na procvičování a otázky.
- Vysvětlení lektorky bylo dobré, lehce pochopitelné.
Reference ze školení Power BI - Expertní úroveň (6/2020)
- Skvěle vysvětleno jak a proč něco funguje. Na tom se dá stavět.
- Líbilo se mi teoretické vysvětlení Power BI, spousta tipů na zefektivnění modelů.
- Dobrý a vyvážený mix DAXu, M a teorie.
- Vysoký skill přednášejícího, ochota odpovídat na individuální dotazy.
- Líbily se mi věci kolem Power Query, které člověk na webu běžně nenajde.
Reference ze školení Excel pro labužníky (3/2020)
- Velmi praktické a jasné vysvětlení Power Query
- Výborné
- Líbily se mi praktické příklady, ochota lektora, řešení skutečných problémů, diskuse
Reference ze školení Power BI prakticky (2/2020)
- Skvělé vysvětlení od základů, srozumitelně, ukázané na příkladech.
- Líbilo se mi vysvětlování dotazů ihned a odbornost kurzu.
- Líbila se mi názornost.
Reference z kurzu Excel pro začátečníky (1/2020)
- Velmi dobrá, ochotná a příjemná lektorka.
- Srozumitelný výklad lektorky, tempo vyhovovalo všem, stihlo se toho hodně oproti původnímu očekávání.
- Naprosto geniální a úžasný kurz. Lektorka je skvělá ve vysvětlování a po dlouhém trápení, co jsem kdy s Excelem měla, jsem pochopila vše, co na kurzu bylo. Velmi děkuji ExcelTown za úžasný kurz.
Reference z kurzu pro Metalimex (11/2019)
- Bylo to super, dobrá komunikace
- Kurz byl perfektně připraven a celá výuka byla podána pro mě naprosto srozumitelným způsobem. Děkuji.
- Každý jsme si řekli, co se potřebujeme naučit, a podle toho se vyučovalo.
Reference ze školení pro ČEZ (1/2020)
- Líbily se mi praktické ukázky.
- Získal jsem celkový přehled o Power BI!
- Líbilo se mi vše.

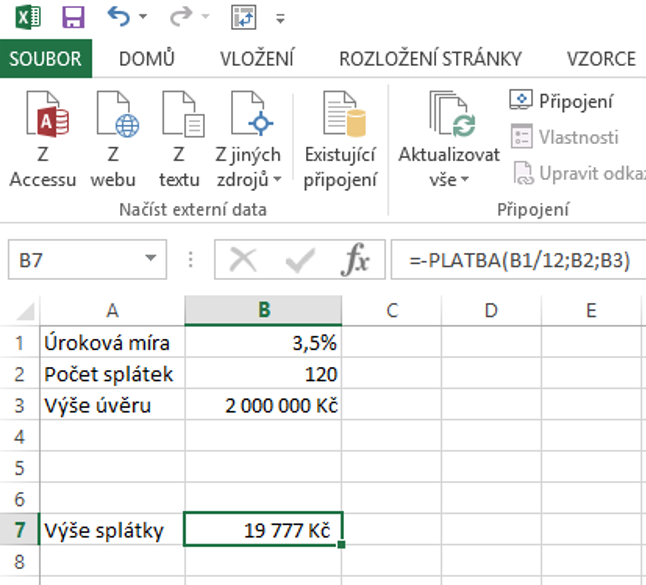
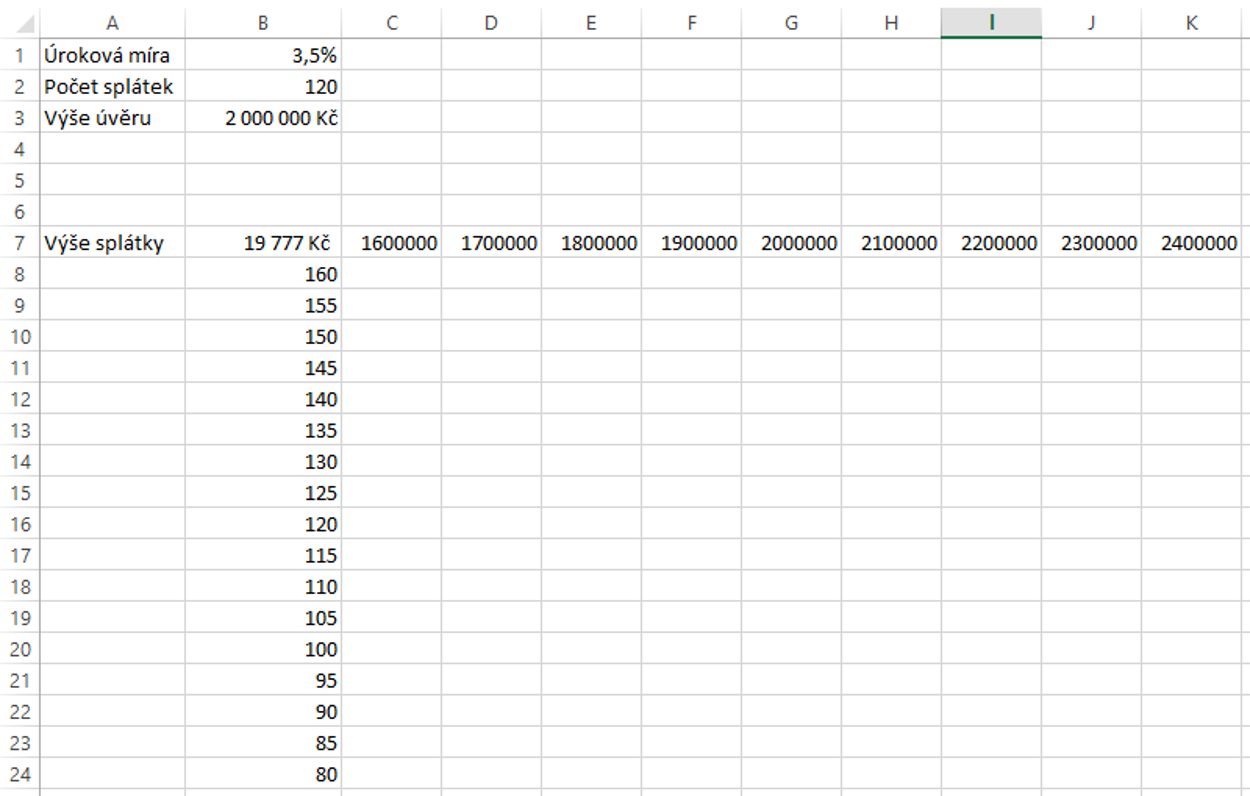
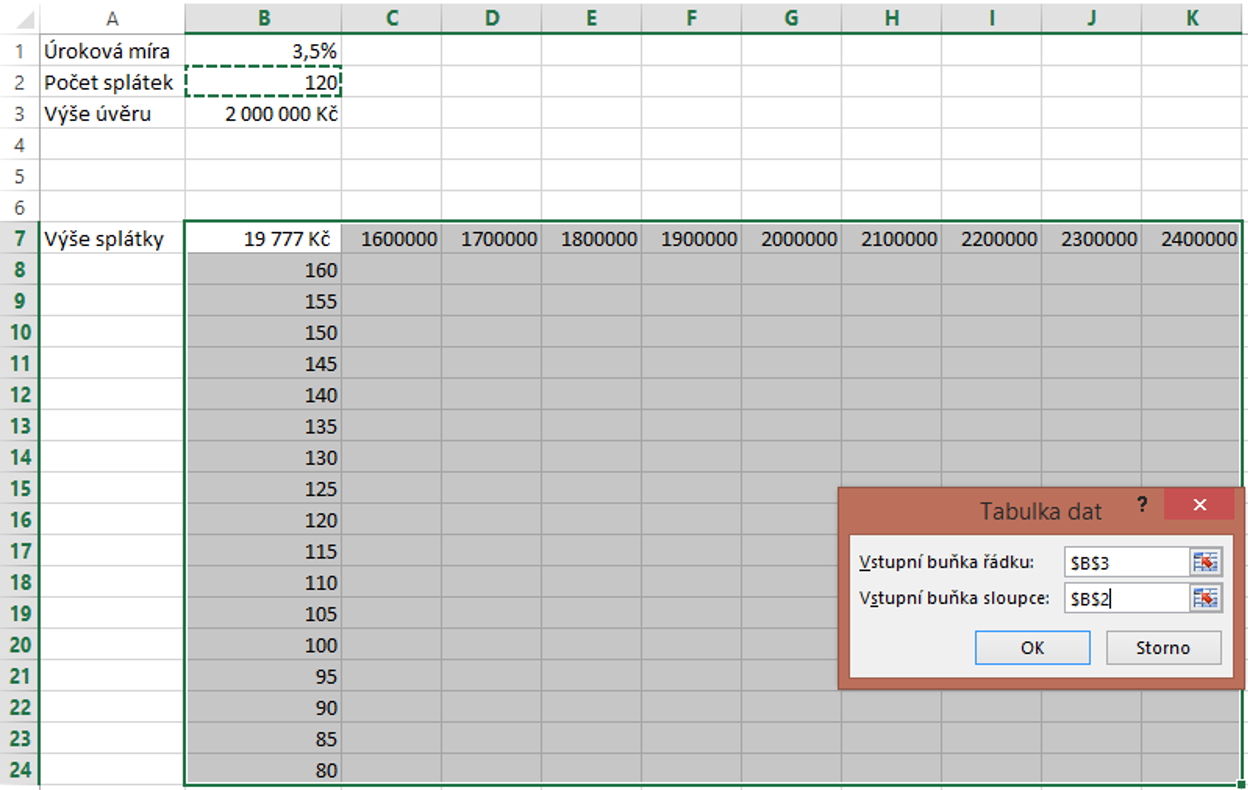
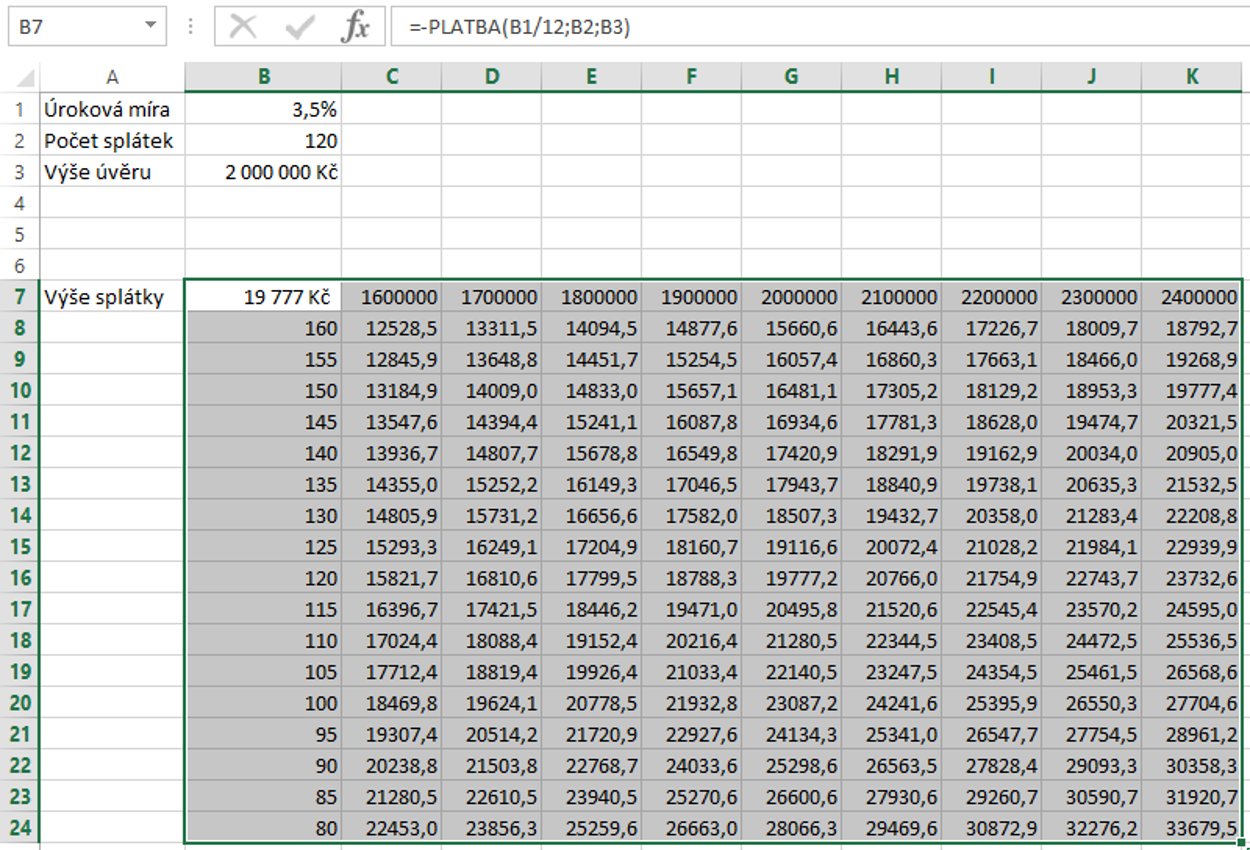
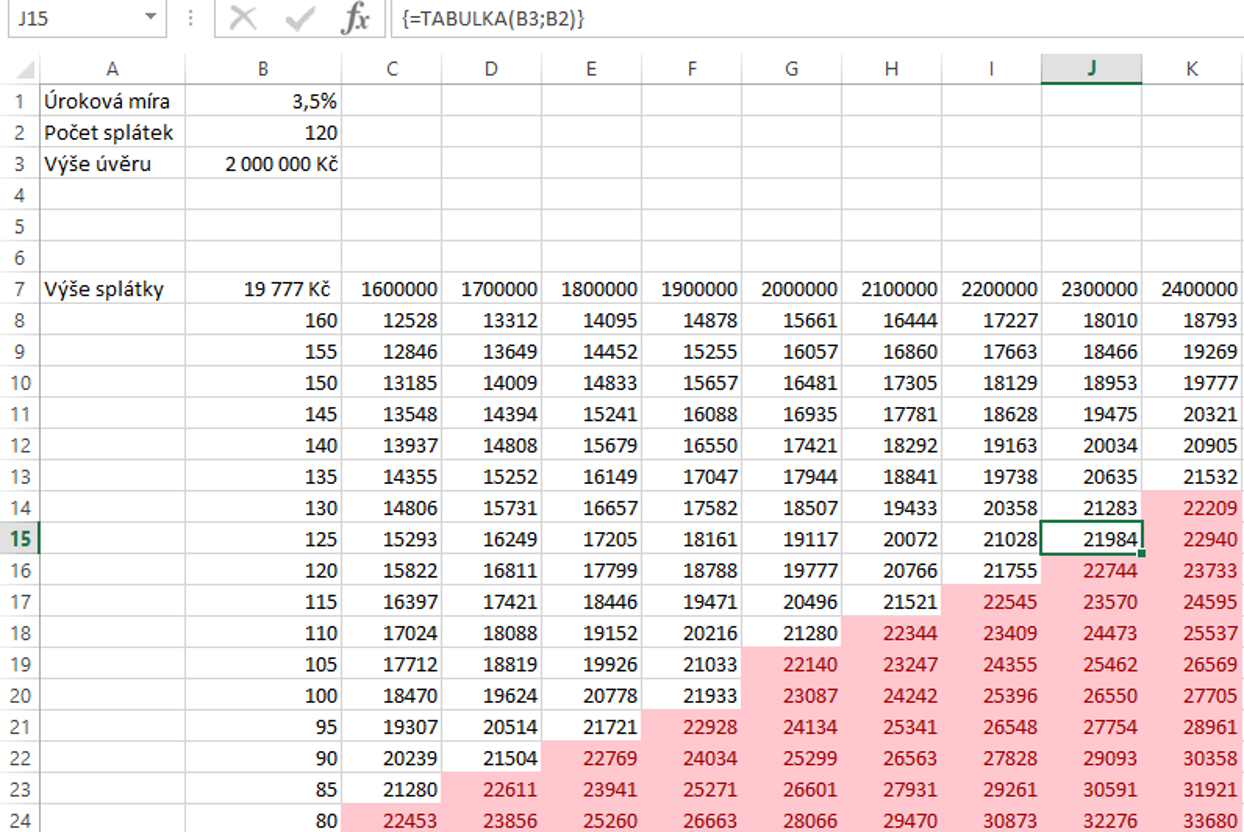
Na Excelu na krásné, že i zdánlivě složité operace jsou skoro až ,,primitivní,, pokud se ví jak na to. Velké DÍK a úcta autorovi, který si dal tu práci a čas, ale hlavně bez složitostí vše popsal.
Jsem rád že se líbí 🙂