Našimi kurzy prošlo více než 10 000+ účastníků
2 392 ověřených referencí účastníků našich kurzů. Přesvědčte se sami
Reference ze školení Středně pokročilý Excel (11/2023)
- Hezky a jednoduše podané příklady
- Přístup paní lektorky byl skvělý
- Zodpovězené dodatečné dotazy
- Skvělý a empatický přístup paní lektorky, naprostá spokojenost
Kurz:
Reference ze školení SQL (10/2023)
- Možnost sama si vše naklikat na PC
- Nezatěžování teorií
- Skvělé vedení kurzu i obsah
- Praktické zkoušení dotazů je super, odbočka k Power Query také
Kurz:
Reference ze školení PYTHON (09/2023)
- Byla jsem s pokojena s lektorem i organizací
- Seznámení a postupné ponoření do problematiky bylo skvělé
- Bavila mě především celá hlavní část kurzu
- Konkrétní příklady byly moc užitečné
- Ideální tempo, srozumitelnosti, praktické příklady
Kurz:
Reference ze školení Středně pokročilý Excel (09/2023)
- Super jsou příklady a cvičení
- Cokoliv nešlo, lektorka pomohla a poradila
- Výklad mentorky byl výborný
- Mnoho praktických příkladů
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (09/2023)
- Způsob vykládání, hodně příkladů, vše jsem si mohla vyzkoušet - vše velmi srozumitelné
- Vyhovovalo mi, že se vše dělalo na příkladech
- Jednoduché vysvětlení, možnost prakticky vyzkoušet
Kurz:
Reference ze školení Středně pokročilý Excel (08/2023)
- Rychlost výkladu akorát
- Dostatek příkladů a procvičování i opakování
- Super tempo
- Flexibilní pojetí výuky
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Středně pokročilý Excel (05/2023)
- Výborná lektorka
- Tempo přizpůsobené všem
- Člověk se nebál zeptat
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (05/2023)
- Kurz je dobře strukturovaný, moc mi to vyhovovalo
- Přístup lektora byl nápomocný, vše dobře vysvětlil
- Vhodné tempo, proaktivní přístup
Kurz:
Reference ze školení Středně pokročilý Excel (03/2023)
- Lektorka byla velmi ochotná
- Vše vysvětlovala v klidu, a když bylo potřeba, cokoliv zopakovala
- Velmi srozumitelné a dobře vysvětleno
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (02/2023)
- Vše bylo vyzkoušeno od úvodu
- Příjemné tempo práce
- Příjemný lektor ochotný vše vysvětlit
- Tempo tak akorát, perfektní přístup, vynikající znalosti
Kurz:
Reference ze školení Excelu pro labužníky (11/2022)
- Oceňuji - nachystané podklady, příklady využitelné v praxi
- Skvělé vychytávky, vyhovující tempo
- Skvělý lektor - profesionální, sympatický
Kurz:
Reference ze školení Úvod do Power BI (11/2022)
- Vše zkoušíme, méně teorie
- Každý zádrhel se vysvětlí :-)
- Praktické příklady, možnost si vše vyzkoušet, tempo lektora - vše super!
- Rychlost je odpovídající náročnosti a zkušenosti školených
- Interaktivita, ukázky chyb (na co si dát pozor), výklad byl jasný a přehledný
- Výborné tempo, skvělý přístup, vynikající znalosti
Kurz:
Reference ze školení Power Query a Power Pivot (10/2022)
- Srozumitelnost přednosu
- Hodně praxe tj.super
- Výborné zkušební příklady
- Tipy v Power Pivot
Kurz:
Kurz Power Query a Power Pivot
Reference ze školení Středně pokročilý Excel (10/2022)
- Pro mě velmi obohacující.
- Spoustu typů a vychytávek. Příjemná lektorka.
- Dostatek času procvičit příklady
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Excelu pro BENU Lékárna (09/2022)
- Lektor byl velmi komunikativní a nápomocný. Kdykoli někdo potřeboval, aby lektor zpomalil, tak ochotně cely usek zopakoval.
- Získal jsem základní přehled o Excelu, Zatím jsem byl samouk.
- Vše super
Reference ze školení SQL (02/2022)
- Výborný a zrozumiteľný spôsob podania
- Paní Šperková velice pěkně vysvětluje a vše je pochopitelné i pro začínající.
- Líbilo se mi podání kurzu ve smyslu příkladů, ukázek různých přístupů a návodů, jak v souvislosti s jazykem SQL přemýšlet. Dobré byly ukázky příkazů pro práci s čísly a textovými řetězci. Výklad byl velmi srozumitelný.
Kurz:
Reference ze školení Excelu (01/2022)
- Oceňuji, že lektor souběžně komentuje, co dělá a promítá to na sdílenou obrazovku, rovněž oceňuji tempo celého procesu
- Jsem začátečník, moc se mi to líbilo.
- Praktické příklady jsou vždy lepší než teorie, takže super.
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (11/2021)
- Za mě dobře vyvážený obsah a vše dobře vysvětleno, dost prostoru na dotazy, dobře připravené příklady.
- Oceňuji, že lektor po krátkém teoretickém úvodu hned přešel k praktickým cvičením, na kterých si člověk mohl lépe uvědomit možnosti programu a principy na kterých pracuje.
- Nemám, co vytknout, je to super :)
Kurz:
Reference ze školení Excelu (11/2021)
- Moje první celodenní školení on line, byla jsem spokojená
- Kurz byl skvělý (není co vytknout, tak alespoň maličkosti :) ), moc děkuji.
- Pan lektor problematiku zná, pracuje s ní v praxi, umí bezvadně podat, nemám jedinou výhradu. Obávám se že není moc prostoru pro další zlepšení.
- Školení mi přineslo to, co jsem očekávala - rozšíření znalostí z excelu, poznání nových funkcí a návod, jak ty stávající používat lépe. Ukázka z Power Pivot mě nalákala na další školení :-)
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Excelu (10/2021)
- Jednotlivé funkce Excelu byly prezentovány názorně a zároveň srozumitelně. Lektorka volila tempo dle potřeb účastníků kurzu, byla velmi příjemná, ochotná pomoci a dovysvětlit.
- Skvěle zvolená struktura kurzu. Výklad jasný a pochopitelný. Velmi milá lektorka.
- Líbilo se mi že jsem si mohla vyzkoušet vše na PC. Pokud jsem měla problém, řešil se hned.
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Excelu (12/2020)
-
Není co vytknout - naprosto srozumitelný výklad.
-
Líbil se mi přístup k jednotlivcům a rady k našim individuálním požadavkům.
-
Líbil jsem mi výklad po obsahové stránce i způsob, jakým byl podán.
Kurz:
https://exceltown.com/kurzy/dvoudenni-stredne-pokrocily-kurz-excelu/
Reference ze školení Úvod do Power BI (9/2020)
- Kurz se mi celkově velmi líbil. Přišla mi dobrá struktura, posloupnost i množství informací
- Dobrý výklad látky, skvělé praktické příklady a ukázky, tipy a triky
- Jasná struktura kurzu - Vizuály / Datový model / Power Query
- Bylo to praktické. Pomůže mi to optimalizovat už vytvořené dotazy
Kurz:
Reference ze školení Excel pro začátečníky (6/2020)
- Vše v nejlepším pořádku.
- Výborný výklad, příklady, odpovědi na otázky...
- Skvělá školitelka, vše bylo srozumitelné.
- Super výuka, nic bych neměnila.
- Základy vysvětleny jednoduše a pochopitelně, dostatek času na procvičování a otázky.
- Vysvětlení lektorky bylo dobré, lehce pochopitelné.
Reference ze školení Power BI - Expertní úroveň (6/2020)
- Skvěle vysvětleno jak a proč něco funguje. Na tom se dá stavět.
- Líbilo se mi teoretické vysvětlení Power BI, spousta tipů na zefektivnění modelů.
- Dobrý a vyvážený mix DAXu, M a teorie.
- Vysoký skill přednášejícího, ochota odpovídat na individuální dotazy.
- Líbily se mi věci kolem Power Query, které člověk na webu běžně nenajde.
Reference ze školení Excel pro labužníky (3/2020)
- Velmi praktické a jasné vysvětlení Power Query
- Výborné
- Líbily se mi praktické příklady, ochota lektora, řešení skutečných problémů, diskuse
Reference ze školení Power BI prakticky (2/2020)
- Skvělé vysvětlení od základů, srozumitelně, ukázané na příkladech.
- Líbilo se mi vysvětlování dotazů ihned a odbornost kurzu.
- Líbila se mi názornost.
Reference z kurzu Excel pro začátečníky (1/2020)
- Velmi dobrá, ochotná a příjemná lektorka.
- Srozumitelný výklad lektorky, tempo vyhovovalo všem, stihlo se toho hodně oproti původnímu očekávání.
- Naprosto geniální a úžasný kurz. Lektorka je skvělá ve vysvětlování a po dlouhém trápení, co jsem kdy s Excelem měla, jsem pochopila vše, co na kurzu bylo. Velmi děkuji ExcelTown za úžasný kurz.
Reference z kurzu pro Metalimex (11/2019)
- Bylo to super, dobrá komunikace
- Kurz byl perfektně připraven a celá výuka byla podána pro mě naprosto srozumitelným způsobem. Děkuji.
- Každý jsme si řekli, co se potřebujeme naučit, a podle toho se vyučovalo.
Reference ze školení pro ČEZ (1/2020)
- Líbily se mi praktické ukázky.
- Získal jsem celkový přehled o Power BI!
- Líbilo se mi vše.

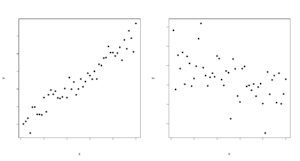
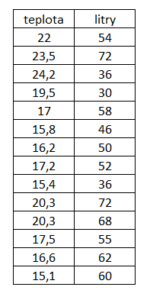
Takže pokud bych měl seřadit těsnot kolerace od nejvolnější po nejtěsnější
Tak by to bylo například 0,03 , -0,06 , -0,24, 0.5 , -0,75 ?
Ano
Dobrý den,
můžu se zeptat kdy nulový koeficient korelace neznamená nezávislost pozorovaných znaků?
Tady už je to trochu mimo moje zaměření, ale myslím že pokud je korelační koeficient kolem nuly, a znaky by měly být významněji závislé, tak to může být pouze malým (nereprezentativním) vzorkem.